Signed Integers are Asymmetrical

What’s wrong with this code?

int8_t absolute(int8_t x) {
  if (x >= 0) {
    return x;
  } else {
    return -x;
  }
}

Seems straightforward enough. Let’s try it with some representative numbers:

#include <stdint.h>
#include <stdio.h>

int8_t absolute(int8_t x) {
  if (x >= 0) {
    return x;
  } else {
    return -x;
  }
}

int main() {
  int8_t values[5] = {INT8_MIN, INT8_MIN + 1, 0, INT8_MAX - 1, INT8_MAX};
  for (int i = 0; i < 5; i++) {
    int8_t x = values[i];
    printf("abs(%4i) = %4i\n", x, absolute(x));
  }
  return 0;
}

Running this code yields:

eudoxia@bullroarer $ gcc cabs.c
eudoxia@bullroarer $ ./a.out
abs(-128) = -128
abs(-127) =  127
abs(   0) =    0
abs( 126) =  126
abs( 127) =  127

The very first case is wrong. Why? Because signed integers are asymmetrical around zero. Note how INT8_MAX is 127, while INT8_MIN is -128. You can think of it in terms of a number line, with the negative side being larger by one:

More generally: if a signed two’s complement number has n bits, the largest number it can represent is 2^{(n - 1)} - 1, while the most negative number it can represent is -2^{(n - 1)}

You can think of unary negation as rotating a number around zero on the number line. Evaluating -(-127) rotates the number and lands on 127:

Evaluating -(-128) rotates the number around zero, but it lands one step beyond INT8_MAX. Because of overflow, it lands right back on INT8_MIN.

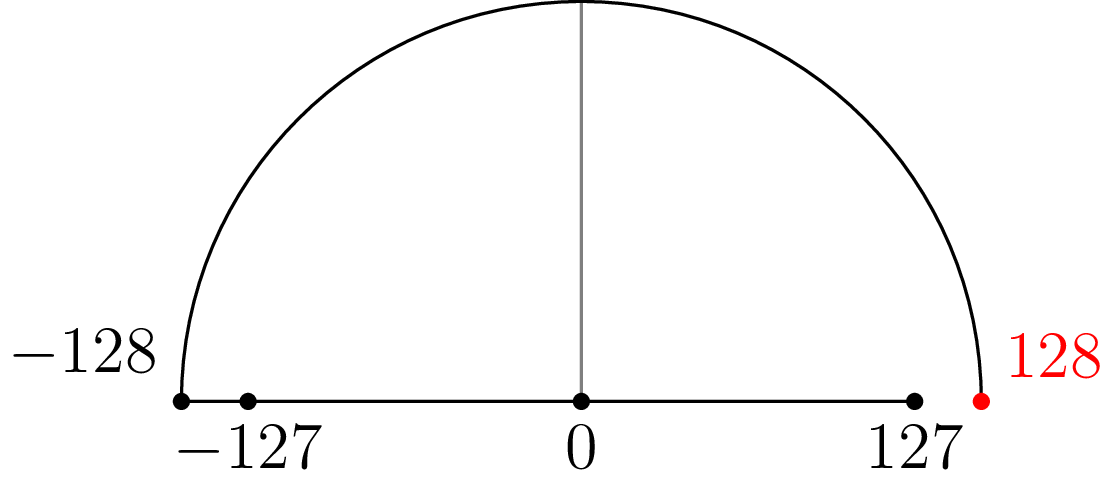
Note that compiling with -ftrapv doesn’t help. Neither GCC nor Clang catch this. Ada does, though:

with Ada.Text_IO;

procedure AdaAbs is
   type Signed_Byte is new Integer range -128 .. 127;

   function Absolute(X: Signed_Byte) return Signed_Byte is
   begin
      if X >= 0 then
         return X;
      else
         return -X;
      end if;
   end Absolute;

   type Index is range 1 .. 5;
   type Value_Array is array (Index) of Signed_Byte;

   Values: Value_Array := (127, 126, 0, -127, -128);

   package Signed_Byte_IO is new Ada.Text_IO.Integer_IO (Signed_Byte);
begin
   for I in Index loop
      declare
         X: Signed_Byte := Values(I);
      begin
         Ada.Text_IO.Put("abs(");
         Signed_Byte_IO.Put(X);
         Ada.Text_IO.Put(") = ");
         Signed_Byte_IO.Put(Absolute(X));
         Ada.Text_IO.New_Line;
      end;
   end loop;
end AdaAbs;

Running this yields:

eudoxia@bullroarer $ gnatmake adaabs.adb
x86_64-linux-gnu-gnatbind-10 -x adaabs.ali
x86_64-linux-gnu-gnatlink-10 adaabs.ali
eudoxia@bullroarer $ ./adaabs
abs( 127) =  127
abs( 126) =  126
abs(   0) =    0
abs(-127) =  127
abs(-128) =

raised CONSTRAINT_ERROR : adaabs.adb:11 range check failed

I only became aware of this issue from an AdaCore case study, probably this, about using SPARK Ada to prove overflow-safety in an implementation of the absolute value function. Here is such an implementation.

This case was a big part of my motivation for having pervasive overflow checking in Austral: the fact that the trivial implementation of the absolute value function – which matches its mathematical definition exactly – is subtly wrong should be humbling, and prove the futility of having programmers mentally track every overflow possibility.

The takeaway: when working with fixed-width integers, test on extremal values. And don’t trust -ftrapv.