I’ve been on a spaced repetition (SR) kick as of late. Mochi, the SR software I use, uses a modified version of the SuperMemo SM-2 algorithm to schedule cards. The differences are:

1. The ease factor (EF) of the cards is not adjusted in response to performance, but can be changed manually. The justification is this avoids a purported problem with SM-2 called “ease hell”.
2. When you fail a card, the interval to the next review is not reset but halved.

The interval halving I dislike, because sometimes I’ll remember a card for the first couple months, then forget it, and enter this weird limbo state where the reviews are not frequent enough for me to re-learn the card, so I start alternately recalling it and failing it.

But I didn’t understand the implications of the change to the ease factor. So I decided to look into the algorithm. And, since what I do not create, I do not understand, I wrote a simple implementation of it in Rust.

Without further ado, the code is here. What follows is an explanation.

The Algorithm

Why do we need an algorithm? We could drill every card every day, but this would be a living nightmare, and you could not have more than ~200 flashcards. The scheduler acts as a simple, quantitative model of human memory. The better the model, the more we can commit to long-term memory, and the less time we have to spend studying.

An item is an atomic piece of knowledge, represented as a flashcard: a question-answer pair that tests the existence of that knowledge. An item’s state is represented by:

1. The easing factor $EF$, which is the dual of difficulty. This is a real number in the range $[1.3, +\infty]$. The initial value is $2.5$.
2. The number of repetitions $n$, which is the number of times the card has been recalled correctly in a row.

From a card’s state, we can calculate its interval: the number of days after the most recent test when the item should be reviewed again. The interval calculation is defined by a recurrence relation on the number of repetitions:

The closed-form expression is:

As a function of correct repetitions and EF:

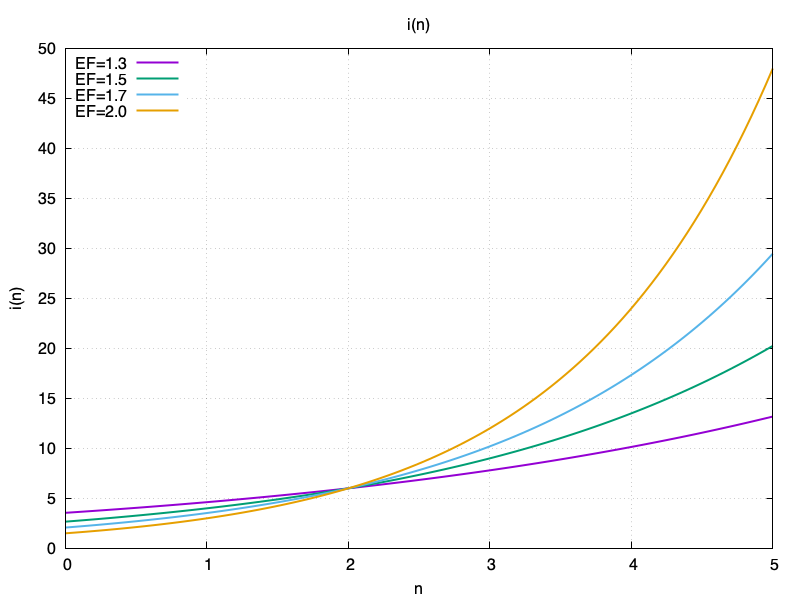
To test an item, the user is shown the question, then they mentally recall the answer, and reveal the actual answer. Then the user rates their performance by selecting the quality of their response from this list:

• 0 = Blackout. No recall.
• 1 = Incorrect response; but the answer, once revealed, was remembered.
• 2 = Incorrect response; but the answer seemed easy to recall.
• 3 = Recalled with difficulty.
• 4 = Recalled with hesitation.
• 5 = Recalled perfectly.

Quality values in $[0,2]$ represent forgetting.

When an item is tested, and we have a quality, the item’s state has to be updated.

If the user forgot the answer, the repetition count is set to zero. This means the interval, too, is reset: you have to relearn the card from scratch.

The EF is updated by adding a magnitude proportional to the response quality:

Where:

Qualitatively, $f(q)$ looks like this:

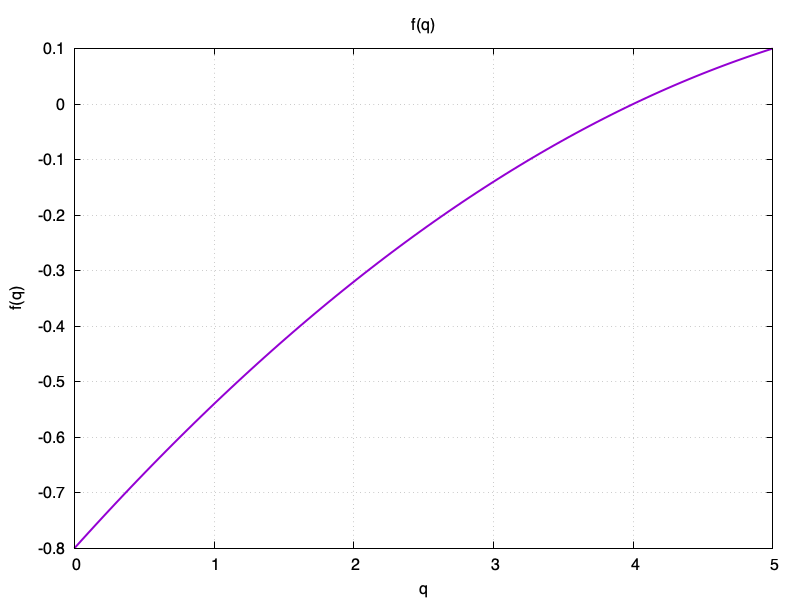
So for anything less than perfect recall the EF decreases (and so the next interval is shorter), and only perfect recall makes a card less difficult. At $q=4$ nothing changes.

And so we get ease hell: it is much easier to push EF down, or keep it the same, than to push it up.

The final piece of the algorithm is that, at the end of a review session, all items with quality in $[0, 3]$ should be tested again until all of them have a recall quality in $[4,5]$.

The Code

Scalar types:

pub type Repetitions = u32;
pub type Ease = f32;
pub type Interval = u32;

Normally I would use newtypes with smart constructors to represent types with ranges (e.g. EF has a minimum value of 1.3). But this would make the code uglier, so instead I just wrote:

pub const INITIAL_EF: Ease = 2.5;
const MIN_EF: Ease = 1.3;

fn min(ef: Ease) -> Ease {
    if ef < MIN_EF {
        MIN_EF
    } else {
        ef
    }
}

Quality is naturally represented as an enum:

#[derive(Debug, Copy, Clone, PartialEq)]
pub enum Quality {
    /// Complete blackout.
    Blackout = 0,
    /// Incorrect response; the correct one remembered.
    Incorrect = 1,
    /// Incorrect response; where the correct one seemed easy to recall.
    IncorrectEasy = 2,
    /// Correct response recalled with serious difficulty.
    Hard = 3,
    /// Correct response after a hesitation.
    Good = 4,
    /// Perfect response.
    Perfect = 5,
}

With two predicates, to test whether this quality value implies the forgetting, and whether the item needs to be repeated at the end of the session:

impl Quality {
    pub fn forgot(self) -> bool {
        match self {
            Self::Blackout
            | Self::Incorrect
            | Self::IncorrectEasy => true,
            Self::Hard | Self::Good | Self::Perfect => {
                false
            }
        }
    }

    pub fn repeat(self) -> bool {
        match self {
            Self::Blackout
            | Self::Incorrect
            | Self::IncorrectEasy
            | Self::Hard => true,
            Self::Good | Self::Perfect => false,
        }
    }
}

An item’s state is just its values of $n$ and $\text{EF}$ (exact due date timestamps would be implemented outside the system):

pub struct Item {
    n: Repetitions,
    ef: Ease,
}

Given an item, we can calculate its interval:

impl Item {
    pub fn interval(&self) -> Interval {
        let r = self.n;
        let ef = self.ef;
        match self.n {
            0 => 0,
            1 => 1,
            2 => 6,
            _ => {
                let r = r as f32;
                let i = 6.0 * ef.powf(r - 2.0);
                let i = i.ceil();
                i as u32
            }
        }
    }
}

The Item::review method consumes an item and, given a quality rating, updates its state:

impl Item {
    pub fn review(self, q: Quality) -> Self {
        Self {
            n: np(self.n, q),
            ef: efp(self.ef, q),
        }
    }
}

Where:

fn np(n: Repetitions, q: Quality) -> Repetitions {
    if q.forgot() {
        0
    } else {
        n + 1
    }
}

fn efp(ef: Ease, q: Quality) -> Ease {
    let ef = min(ef);
    let q = (q as u8) as f32;
    let ef = ef - 0.8 + 0.28 * q - 0.02 * q * q;
    min(ef)
}

Edit 2024-12-28: correction, Mochi doesn’t use SM-2. I was reading their old FAQ, which as of right now is still indexed on Google. The current FAQ says they use a simpler system where the interval is multiplied by a number $>1$ on success and by a number in $[0,1]$ on failure.