A while back I wrote an implementation of SM-2, the algorithm used by Anki to schedule flashcard reviews. While reading up on it I heard about FSRS, a new algorithm that is slated to replace SM-2 as Anki’s default scheduler. The pitch for FSRS is efficiency: 30% less review time for isoretention compared to SM-2. So I got curious.

Initially I had difficulty understanding FSRS, because the information about it is scattered all over the place: GitHub wikis, blogs, Reddit. On top of that there are different versions of the algorithm, and sources don’t always specify which one they talk about.

So I put everything I could find together, and cleaned it up. The implementation turned out to be just 100 lines, though much of it remains cryptic: while SM-2 was intelligently designed, FSRS was evolved by training a model on a dataset of Anki reviews. But you don’t need a PhD in machine learning to understand the implementation.

The rest of this post explains the theory of FSRS, with equations interleaved with Rust code. If you just want the code, scroll to the end. The repository is here.

The DSR Model

FSRS is based on the 3-component model of memory, also called the DSR model. Under DSR, the state of a memory in the brain is modeled by three variables:

Retrievability ($R$) is the probability of recalling the memory. This is a real number in the range $[0, 1]$.

type R = f64;

Stability ($S$) is the time in days for $R$ to go from $1$ to $0.9$ (i.e. 90% probability). This is a real number in the range $[0, +\infty]$.

type S = f64;

Difficulty ($D$) models how hard it is to recall the memory. This is a real number in $[1, 10]$. Note that we start at $1$, not $0$.

type D = f64;

When implementing the algorithm, retrievability is computed dynamically, while stability and difficulty are properties of the card object.

The Main Loop

The main loop of the algorithm is:

1. For each card due today:
   1. Show the user the question.
   2. User mentally recalls the answer, and flips the card.
   3. User rates their recall performance on the card.
   4. The algorithm updates the card’s stability and difficulty values, calculates the next review interval, and schedules the card for that day.

We’re focused on implementing the last step: in response to a user’s performance, update the state of the card and schedule it for the next review.

The user’s self-rating of recall performance is called the grade, and it’s one of:

• 1 = forgot the answer (“forgot”).
• 2 = recalled the answer, but it was hard (“hard”)
• 3 = recalled the answer (“good”)
• 4 = recalled the answer, and it was easy (“easy”)

#[derive(Clone, Copy, PartialEq, Debug)]
enum Grade {
    Forgot,
    Hard,
    Good,
    Easy,
}

impl From<Grade> for f64 {
    fn from(g: Grade) -> f64 {
        match g {
            Grade::Forgot => 1.0,
            Grade::Hard => 2.0,
            Grade::Good => 3.0,
            Grade::Easy => 4.0,
        }
    }
}

Retrievability

The retrievability of a card is approximated by:

Where $t$ is time in days since the last review, $S$ is the stability of the card, and $F$ and $C$ are constants to control the shape of the curve:

This allows us to predict how retrievability decays over time as a function of time and stability. In code:

type T = f64;

const F: f64 = 19.0 / 81.0;
const C: f64 = -0.5;

fn retrievability(t: T, s: S) -> R {
    (1.0 + F * (t / s)).powf(C)
}

Graphically, the forgetting curves for different values of $S$ look like this:

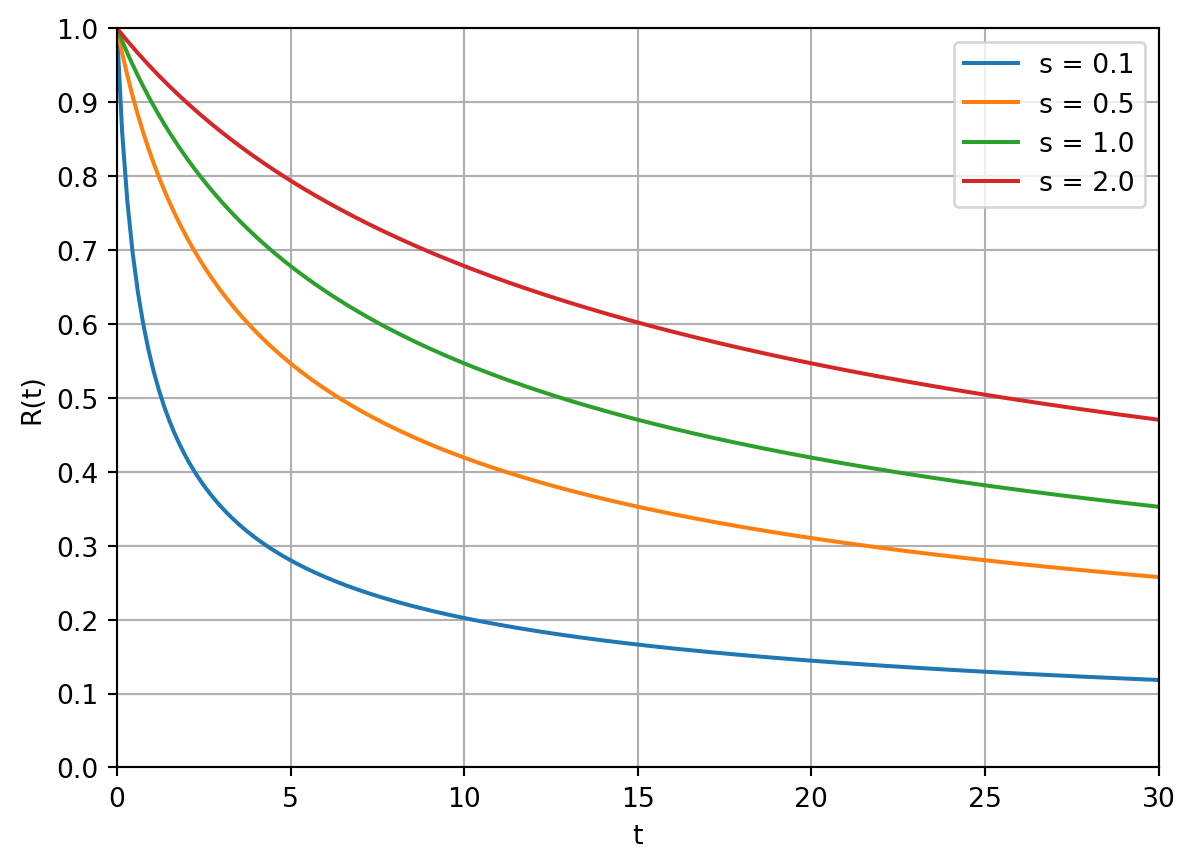
Note that at $t=0$, the equation simplifies to $R(0) = 1$, that is, when we have just seen a card, we have a 100% chance of recalling it.

Review Intervals

The equation for the review interval is found by manipulating the definition of retrievability. Starting from this:

The idea is that this equation gives us “retrievability at time $t$”, but we can rearrange it to instead find “time at which retrievability decays to a given value”. That value is the desired retention. The idea behind FSRS scheduling is that review should happen when predicted retrievability hits desired retention. If desired retention is $0.9$, and you do all your reviews on schedule, then the probability that you will recall a card will always oscillate between 100% and 90%. Which is pretty good.

So, we want to express $t$ in terms of $R$. So we exponentiate both sides by $1/C$:

And move everything left:

And rename things to make this clearer:

Given the desired retention, and the stability of a card, we can calculate when it should next be reviewed.

fn interval(r_d: R, s: S) -> T {
    (s / F) * (r_d.powf(1.0 / C) - 1.0)
}

Intervals grow linearly with stability, for different values of $R_d$:

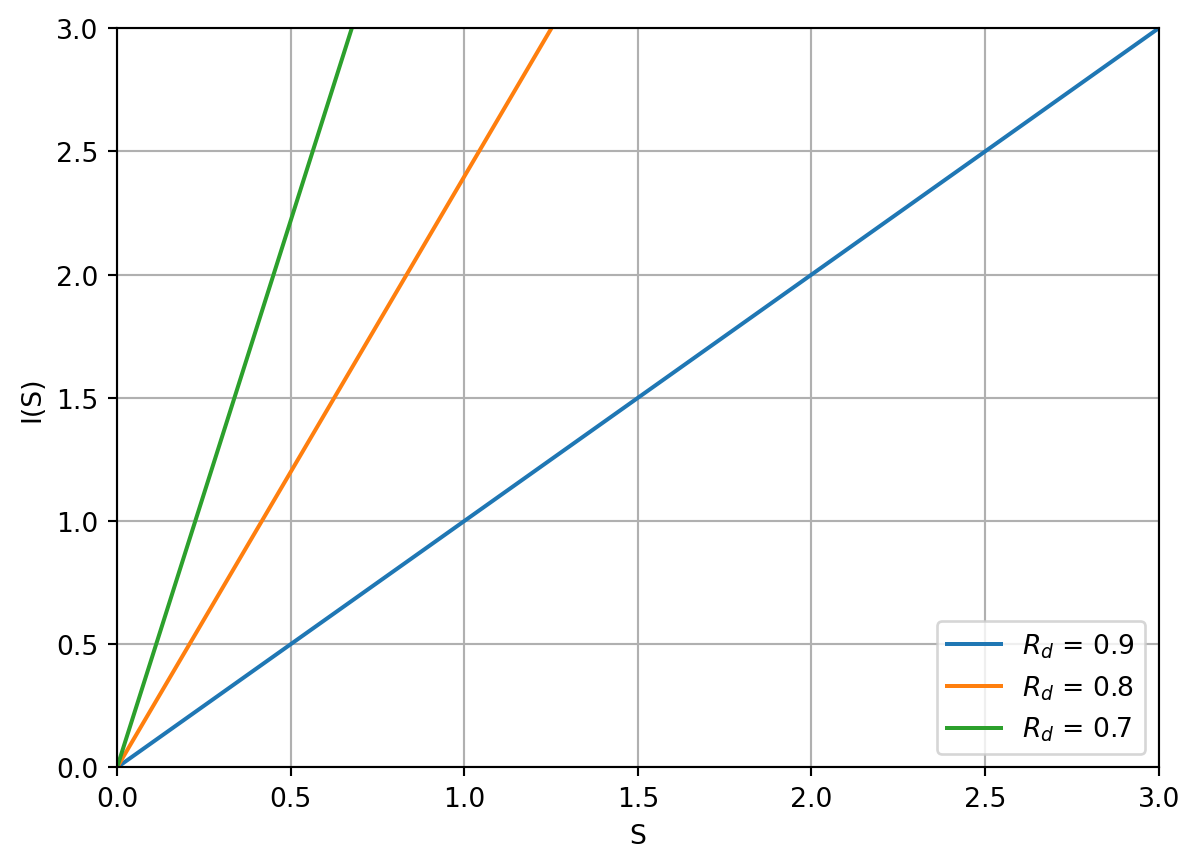
Two things to note:

• At higher $R_d$, reviews will be more frequent, which is what we expect.
• Stability is defined as the interval where $R$ will equal $0.9$. So, for $R_d = 0.9$, $I(S) = S$ by definition, and so the line is at $45^\circ$.

Parameters

The algorithm has 19 learned parameters, with the following defaults:

pub const W: [f64; 19] = [
    0.40255, 1.18385, 3.173, 15.69105, 7.1949, 0.5345, 1.4604, 0.0046, 1.54575, 0.1192, 1.01925,
    1.9395, 0.11, 0.29605, 2.2698, 0.2315, 2.9898, 0.51655, 0.6621,
];

Most of these are used once and have a specific role, so they could be assigned to named constants instead, but I’m keeping them in an array to keep the presentation short.

Updating Stability

This section describes how a card’s stability is updated after a review.

First Time

The first time the user reviews a card, its initial stability is:

That is, the parameters $w_0$ to $w_3$ represent the initial values of stability for a given initial grade. In code:

fn s_0(g: Grade) -> S {
    match g {
        Grade::Forgot => W[0],
        Grade::Hard => W[1],
        Grade::Good => W[2],
        Grade::Easy => W[3],
    }
}

Note that a card that has never been reviewed has no stability.

Stability on Success

Stability is updated differently depending on whether the user forgot ($G=1$) or remembered ($G \in [2,3,4]$) the card. The equation is very big, so I’m going to break it down hierarchically.

After a review, stability is updated by multiplying it by a scaling factor $\alpha$:

Where:

The addition is because some of the multiplicative terms may be zero, and in that case, $\alpha=1$.

$t_d$ is the “difficulty penalty”, defined by:

Harder cards (higher $D$) increase stability more slowly. The highest difficulty is $D=10$, here, $d=1$ and therefore difficulty provides no boost. This is intuitive: harder cards are harder to consolidate.

$t_s$ determines how today’s stability affects the next stability:

If $S$ is high, updates will be smaller. The more stable a memory is, the harder it is to make it more stable. Memory stability saturates.

$t_r$ is about the saturation of retrievability:

If $R=1$ (100% recall) then $t_r=0$. So $\alpha$ as a whole is $1$, i.e. stability does not change. The lower $R$ is, the higher $\alpha$ will be. So the optimal time to review some material is when you have almost forgotten it. Which is somewhat counterintuitive, but it makes sense: the more you remember something, the fewer the gains from reviewing, dually, the more you have forgotten it, the more room there is to improve.

$h$ is the hard penalty:

If recall was hard, we apply $w_{15}$ (a learned parameter between 0 and 1). This penalizes stability growth where recall was shaky. Otherwise, it has no effect.

$b$ is the opposite of $h$, a bonus for easy recall:

If recall was easy, we multiply by $w_{16}$, a number greater than one, which scales stability up. Otherwise, it has no effect.

Finally, the $e^{w_8}$ term just applies a learned parameter to control the shape of the curve.

Putting it all together:

fn s_success(d: D, s: S, r: R, g: Grade) -> S {
    let t_d = 11.0 - d;
    let t_s = s.powf(-W[9]);
    let t_r = f64::exp(W[10] * (1.0 - r)) - 1.0;
    let h = if g == Grade::Hard { W[15] } else { 1.0 };
    let b = if g == Grade::Easy { W[16] } else { 1.0 };
    let c = f64::exp(W[8]);
    let alpha = 1.0 + t_d * t_s * t_r * h * b * c;
    s * alpha
}

Stability on Failure

The formula is different if the user forgot a card:

$\min$ is there to ensure that stability at failure cannot be greater than $S$.

$S_f$, stability on failure, is defined by:

Where:

$d_f$ is the difficulty term, a value in $[0,1]$. Higher $D$ leads to smaller $d_f$, that is, more difficult cards experience a steeper stability loss.

$s_f$ is the stability term, qualitatively, higher $S$ means higher $s_f$, meaning the stable cards lose stability more slowly.

$r_f$ is the retrievability term. Low values of $R$ lead to large positive updates. As $R$ increases, $r_f$ converges to $1$. To be honest I’m not sure I understand this term. I think it’s meant to model the fact that, the lower the predicted retrievability, the less it tells us about stability, since at low values of $R$ you expect the user to have forgotten the card.

Finally, $w_{11}$ is another learned parameter to control the shape of the curve.

Or, in code:

fn s_fail(d: D, s: S, r: R) -> S {
    let d_f = d.powf(-W[12]);
    let s_f = (s + 1.0).powf(W[13]) - 1.0;
    let r_f = f64::exp(W[14] * (1.0 - r));
    let c_f = W[11];
    let s_f = d_f * s_f * r_f * c_f;
    f64::min(s_f, s)
}

Putting it all together:

fn stability(d: D, s: S, r: R, g: Grade) -> S {
    if g == Grade::Forgot {
        s_fail(d, s, r)
    } else {
        s_success(d, s, r, g)
    }
}

Updating Difficulty

This section describes how a card’s difficulty is updated after a review.

First Time

Analogously with stability: a card that has never been reviewed has no difficulty.

The initial difficulty, after the first review, is defined by:

In Rust:

fn d_0(g: Grade) -> D {
    let g: f64 = g.into();
    clamp_d(W[4] - f64::exp(W[5] * (g - 1.0)) + 1.0)
}

fn clamp_d(d: D) -> D {
    d.clamp(1.0, 10.0)
}

clamp_d is there to ensure difficulty never leaves the range (which can’t really be done otherwise). Normally I would use newtypes with validating constructors to represent ranged values, but for this, it would add way too much overhead for what is meant to be a pedagogical implementation.

Note that when $G=1$ (forgot), then $D_0(1) = w_4$, that is, $w_4$ is the initial difficulty of a card when its first review was a failure.

$n$-th time

For any review other than the first, difficulty is updated by:

In code:

fn difficulty(d: D, g: Grade) -> D {
    clamp_d(W[7] * d_0(Grade::Easy) + (1.0 - W[7]) * dp(d, g))
}

fn dp(d: D, g: Grade) -> f64 {
    d + delta_d(g) * ((10.0 - d) / 9.0)
}

fn delta_d(g: Grade) -> f64 {
    let g: f64 = g.into();
    -W[6] * (g - 3.0)
}

And visually:

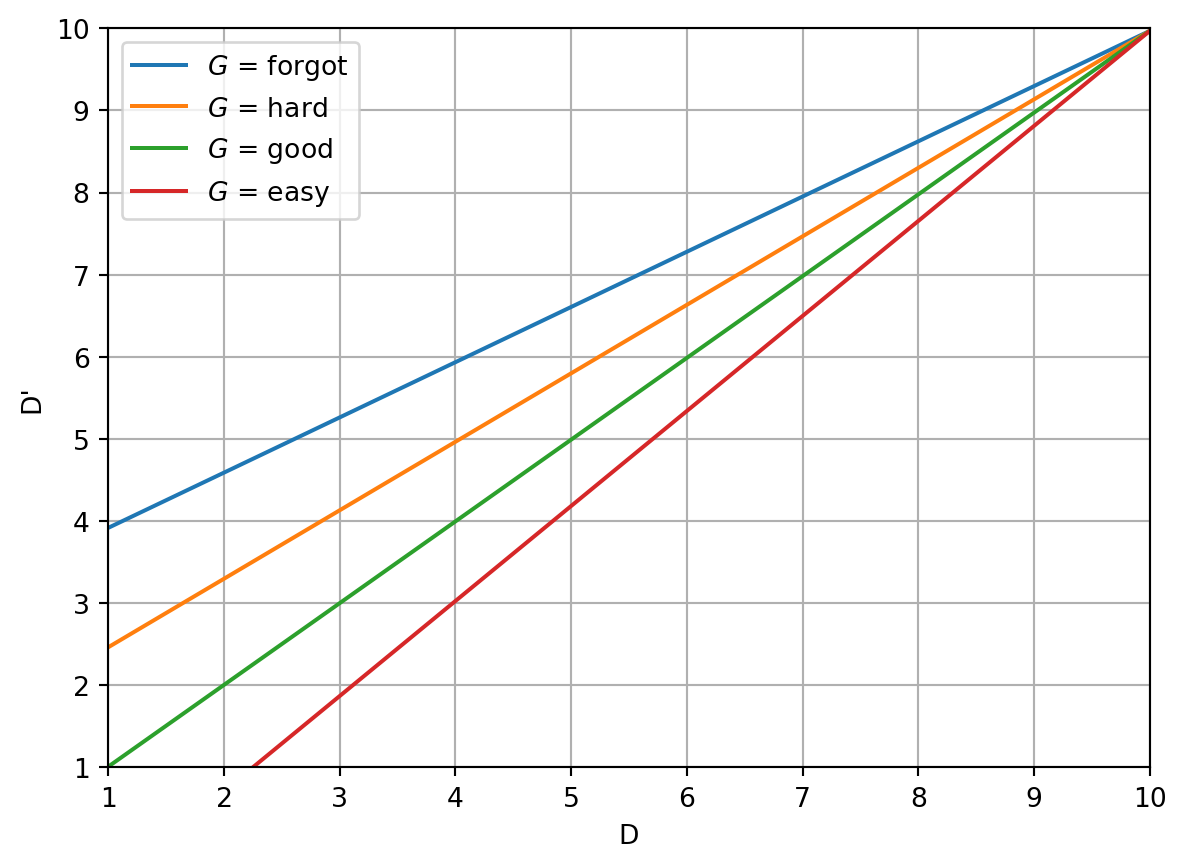
Hitting “good” leaves difficulty unchanged: the line where $G = \text{good}$ has $D’=D$. The $G = \text{easy}$ line has positive slope, difficulty decreases, e.g. if $D=4$ then $D’=3$. The $G = \text{hard}$ and $G = \text{forgot}$ lines have negative slope, so difficulty increases, e.g. forgetting a card with difficulty $3$ pushed the next difficulty to just above $4$.

The Simulator

That’s it. That’s all you need to implement an SR app that uses FSRS.

But the equations are still kind of inscrutable. How can we convince ourselves that the algorithm works correctly?

As far as I know, there are no test vectors for FSRS. But there is a visualizer that lets you see for stability, difficulty, and the review intervals evolve for a given sequence of grades. So, let’s build a simulation tool.

The simulator takes a list of grades, where the $n$-th grade represents the user’s rating on the $n$-th review of a card, and returns a table where each row represents the state of the card after the review:

fn sim(grades: Vec<Grade>) -> Vec<Step> {
  // ...
}

struct Step {
    /// The time when the review took place.
    t: T,
    /// New stability.
    s: S,
    /// New difficulty.
    d: D,
    /// Next interval.
    i: T,
}

We model the user as reviewing everything exactly when the algorithm schedules it, so we don’t need to pass any other values.

The high-level structure of the simulator is:

fn sim(grades: Vec<Grade>) -> Vec<Step> {
    let mut steps = vec![];

    // <initial state>

    // <initial review>

    // <n-th review>

    steps
}

For the initial state, we start at $t=0$ and set $R_d = 0.9$:

let mut t: T = 0.0;
let r_d: f64 = 0.9;

For the initial review, we call s_0 and d_0 to calculate the initial values of stability and difficulty:

assert!(!grades.is_empty());
let mut grades = grades.clone();
let g: Grade = grades.remove(0);
let mut s: S = s_0(g);
let mut d: D = d_0(g);

We then calculate the interval and round it to discretize the review time into a number of days in the future, and use max to ensure the shortest review interval is one day (otherwise, selecting “forget” would yield an interval within the same day).

let mut i: T = f64::max(interval(r_d, s).round(), 1.0);

And record the first step:

steps.push(Step { t, s, d, i });

The $n$-th review is the same as the initial, but we must first calculate $R$:

for g in grades {
  t += i;
  let r: R = retrievability(i, s);
  s = stability(d, s, r, g);
  d = difficulty(d, g);
  i = f64::max(interval(r_d, s).round(), 1.0);
  steps.push(Step { t, s, d, i });
}

Putting it together:

fn sim(grades: Vec<Grade>) -> Vec<Step> {
    let mut t: T = 0.0;
    let r_d: f64 = 0.9;
    let mut steps = vec![];

    // Initial review.
    assert!(!grades.is_empty());
    let mut grades = grades.clone();
    let g: Grade = grades.remove(0);
    let mut s: S = s_0(g);
    let mut d: D = d_0(g);
    let mut i: T = f64::max(interval(r_d, s).round(), 1.0);
    steps.push(Step { t, s, d, i });

    // n-th review
    for g in grades {
        t += i;
        let r: R = retrievability(i, s);
        s = stability(d, s, r, g);
        d = difficulty(d, g);
        i = f64::max(interval(r_d, s).round(), 1.0);
        steps.push(Step { t, s, d, i });
    }

    steps
}

The Code

And without further ado, this is the complete code for the scheduler:

const W: [f64; 19] = [
    0.40255, 1.18385, 3.173, 15.69105, 7.1949, 0.5345, 1.4604, 0.0046, 1.54575, 0.1192, 1.01925,
    1.9395, 0.11, 0.29605, 2.2698, 0.2315, 2.9898, 0.51655, 0.6621,
];

type R = f64;
type S = f64;
type D = f64;

#[derive(Clone, Copy, PartialEq, Debug)]
enum Grade {
    Forgot,
    Hard,
    Good,
    Easy,
}

impl From<Grade> for f64 {
    fn from(g: Grade) -> f64 {
        match g {
            Grade::Forgot => 1.0,
            Grade::Hard => 2.0,
            Grade::Good => 3.0,
            Grade::Easy => 4.0,
        }
    }
}

type T = f64;

const F: f64 = 19.0 / 81.0;
const C: f64 = -0.5;

fn retrievability(t: T, s: S) -> R {
    (1.0 + F * (t / s)).powf(C)
}

fn interval(r_d: R, s: S) -> T {
    (s / F) * (r_d.powf(1.0 / C) - 1.0)
}

fn s_0(g: Grade) -> S {
    match g {
        Grade::Forgot => W[0],
        Grade::Hard => W[1],
        Grade::Good => W[2],
        Grade::Easy => W[3],
    }
}

fn s_success(d: D, s: S, r: R, g: Grade) -> S {
    let t_d = 11.0 - d;
    let t_s = s.powf(-W[9]);
    let t_r = f64::exp(W[10] * (1.0 - r)) - 1.0;
    let h = if g == Grade::Hard { W[15] } else { 1.0 };
    let b = if g == Grade::Easy { W[16] } else { 1.0 };
    let c = f64::exp(W[8]);
    let alpha = 1.0 + t_d * t_s * t_r * h * b * c;
    s * alpha
}

fn s_fail(d: D, s: S, r: R) -> S {
    let d_f = d.powf(-W[12]);
    let s_f = (s + 1.0).powf(W[13]) - 1.0;
    let r_f = f64::exp(W[14] * (1.0 - r));
    let c_f = W[11];
    let s_f = d_f * s_f * r_f * c_f;
    f64::min(s_f, s)
}

fn stability(d: D, s: S, r: R, g: Grade) -> S {
    if g == Grade::Forgot {
        s_fail(d, s, r)
    } else {
        s_success(d, s, r, g)
    }
}

fn clamp_d(d: D) -> D {
    d.clamp(1.0, 10.0)
}

fn d_0(g: Grade) -> D {
    let g: f64 = g.into();
    clamp_d(W[4] - f64::exp(W[5] * (g - 1.0)) + 1.0)
}

fn difficulty(d: D, g: Grade) -> D {
    clamp_d(W[7] * d_0(Grade::Easy) + (1.0 - W[7]) * dp(d, g))
}

fn dp(d: D, g: Grade) -> f64 {
    d + delta_d(g) * ((10.0 - d) / 9.0)
}

fn delta_d(g: Grade) -> f64 {
    let g: f64 = g.into();
    -W[6] * (g - 3.0)
}

See Also

• Description of the algorithm
• FSRS visualizer